Resources: Find Jupiter's Moons App, WolframAlpha

Terminology: Small-Angle Formula, Kepler's Third Law, Percent Error Formula, Eccentricity, Semi-Major Axis, Orbital Period

Jupiter's main moons

Exercises

  • Determine the distance from Earth to Jupiter at the time of the observation.
     
  • Find the semi-major axis for the orbit around Jupiter of the moon whose period you found in the previous section. Remember that the pixel scale of the images is 1"/pixel.
     

  • Find the mass of Jupiter using Kepler's Third Law, described below.

     

  • Convert the mass of Jupiter from solar masses to Earth masses.
     
  • Once you have found your answer, look up Jupiter's actual mass in WolframAlpha so you can calculate your Percent Error. How might you improve your accuracy?

Kepler's Third Law

Kepler discovered that the size of a planet's orbit (the semi-major axis of the ellipse) is simply related to sidereal period of the orbit. He found that if the semi-major axis of the orbit is expressed in astronomical unit, and its period expressed in years, then the square if the period is equal to the semi-major axis cubed. With the application of Newton's laws of motion and gravity, this same idea can be expanded to work for any pair of orbiting bodies. The general form of Kepler's Third Law is:

 

kepler3-2

 

semi-majoraxis

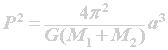
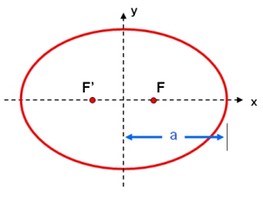
where M1 and M2 are the masses of the two bodies, P is the orbital period, a is the semi-major axis, and G is the gravitational constant (6.673 × 10-11 m3 kg-1 s-2).  Note that if the mass of one body, such as M1, is much larger than the other one, then M1+M2 is nearly equal to M1.

Therefore, in order to make a mass estimation of Jupiter, we need to know the orbital period and semi-major axis of one of its satellites.

Guideposts

  • The eccentricities of the orbits of the Galilean moons are very close to zero, meaning the orbits are nearly circular. They look elliptical because from Earth we are seeing them close to edge-on.