Kepler discovered that the size of a planet's orbit (the semi-major axis of the ellipse) is simply related to sidereal period of the orbit. If the size of the orbit (a) is expressed in astronomical units (1 AU equals the average distance between the Earth and the Sun) and the period (P) is measured in years, then Kepler's Third Law says:
After applying Newton's Laws of Motion and Newton's Law of Gravity we find that Kepler's Third Law takes a more general form:
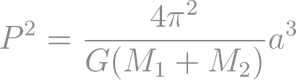
where M1 and M2 are the masses of the two orbiting objects in solar masses. Note that if the mass of one body, such as M1, is much larger than the other, then M1+M2 is nearly equal to M1. In our solar system M1 = 1 solar mass, and this equation becomes identical to the first.
Example Question
Phobos orbits Mars with an average distance of about 9380 km from the center of the planet and a rotational period of about 7hr 39 min. Use this information to estimate the mass of Mars.
Solution
a = 9380 km = 9.38 x 106 m
P = 7 hr 39 min = 7.65 hr = 27540 sec
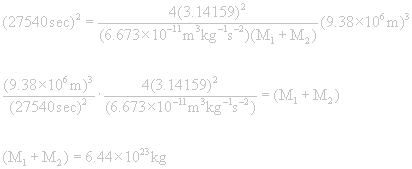
Since the mass of Mars is so much greater than the mass of Phobos, (M1 + M2) is very nearly equal to the mass of Mars, so this is a good estimate.