Resources: Worksheet, compass

Terminology: Small Angle Formula, Stellar Parallax, Angular Resolution

Demonstrations: Parallax, Spectroscopic Parallax, Parallax Calculator

Angular Size

Whenever you look at an object, you are measuring its angular size - the amount of space it takes up in your field of view in degrees, minutes, and seconds (or radians). You can't directly measure an object's size in centimeters or inches unless you walk up to it and use a ruler. You know that faraway objects look small and nearby objects look big, so your brain puts together an object's angular size with your guess as to its distance to give you an idea of its actual size.

Complex and precise instruments exist and can be constructed for measuring the angular size of objects, but a set of rough measurement tools can be found at the end of most people's arms. Because humans are built to mostly the same proportions, if you hold your arms outstretched with your palms facing forward, your hands will have about the same angular size in your field of vision regardless of whether you are tall, short, big or small. Your fingers and knuckles can be used to make rough measurements of angular sizes and distances on the sky as shown in the diagram to the right.

Other useful angular size rulers exist as well. For example, the moon is almost exactly one-half degree in extent as viewed from the surface of the Earth.

Parallax

The apparent size and distance of objects relative to one another change depending on the distance of the objects from the observer. This observed relationship is called parallax. The apparent size, or angular size, is proportional to the linear size (d) and inversely proportional to the distance (D) to the object, or θ ~d/D. The use of parallax was one of the earliest methods used by astronomers for estimating the distances to objects in the solar system, and later nearby stars.

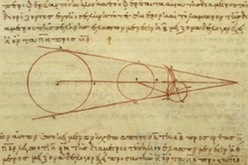
The Greek astronomer Aristarchus was one of the earliest to explain parallax mathematically, and tried to apply this relationship to estimate the distances of the Moon and Sun from the Earth and their relative sizes. Aristarchus would use his findings on parallax in developing one of the first known heliocentric models of the universe. The mathematician Hipparchus, who developed the first trigonometric tables, would later improve on Aristarchus' technique.

In 1989 the European Space Agency (ESA) launched the Hipparcos satellite. Over the course of three years Hipparcos measured the parallax and velocities of over 100,000 stars in our galaxy, with a precision of 0.97 milliarcseconds. 

Parallax is useful for measuring distances to celestial objects and is the first step in building the cosmic distance ladder. Since Hipparcos, Hubble Space Telescope, launched in 1992, has measured the parallax of stars within 1000 parsecs, and GAIA, launched in 2013, is able to measure the parallax of stars within 10,000 parsecs. For even more distant objects, the parallactic angle becomes increasing smaller and more difficult to measure. Estimating these distances then requires other methods like the use of Cepheid variables and the measuring of an object's redshift.