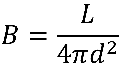Learning Goals: Students will learn how astronomers accurately measure the brightness of stars, as well as how the flux of a star through different colored filters can reveal its temperature. They will then use the brightness and temperature of stars to make inferences about their properties.
Suggested Observations: B, V image of an evolved open cluster such as M67
Challenge: Your team will take images of an open cluster - a group of stars that formed together at roughly the same time. You will measure the apparent magnitude of several stars and calculate their surface temperature.