Terminology: Stellar Parallax, Percent Error Formula 

Introduction to Parallax:

Hold out your hand at arm’s length and look at your thumb with one eye closed. Then close that eye and open the other. Did your thumb appear to move? This apparent displacement is called parallax and is useful for determining the distance to objects.

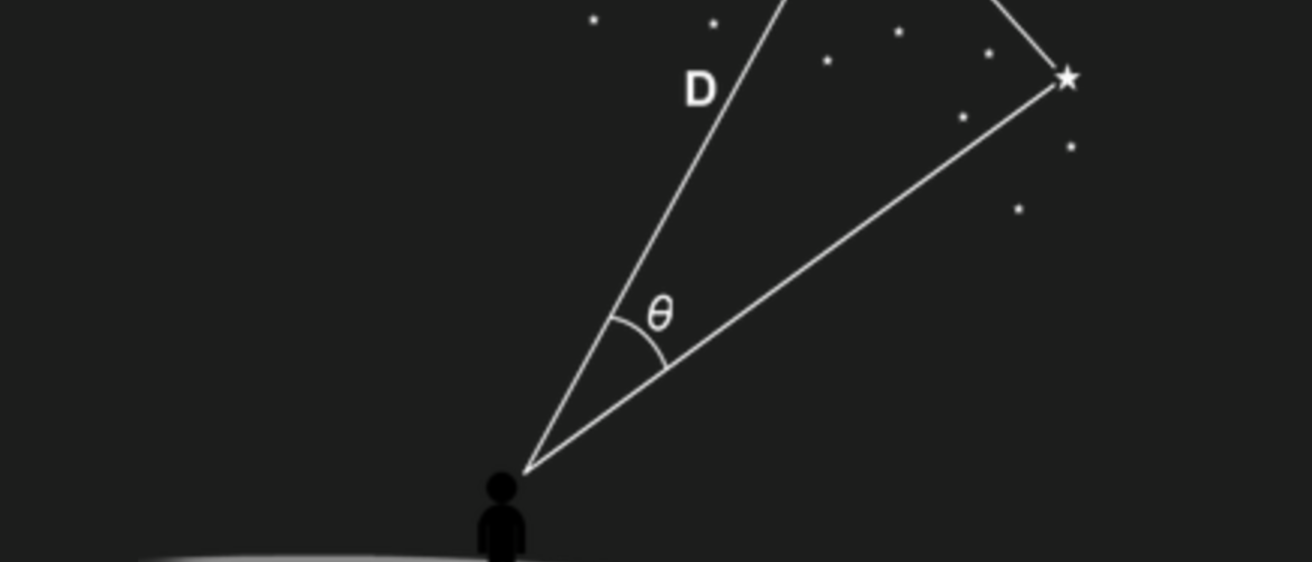
Consider the figure below. The two observers will perceive the object at different places relative to the distant background by an angle θ. If two observers are a distance S apart, the object is a distance D away, and the distance D is much larger than S, then the small angle formula can be used to relate S and D, so that θ_rad = S/D, where θ_rad is given in radians. As 57.3° is approximately equal to 1 radian, this can be converted to a relationship in degrees: θdegree = 57.3° S/D.

If we measure the angle θ and the distance S between the two observers, we can estimate the distance D to the object using the above formulas. The first formula works when measuring the angle in radians; the second formula works when θ is in degrees. 

In this part, we’ll measure the distance to our pinky from our eyes when our arm is fully extended.

1. What parallax angle θ does your pinky make when held at arm’s length?

2. Measure the distance S between the pupils of your eyes in centimeters. Record your answer below.

3. Using your parallax angle θ, and the distance S between the pupils of your eyes, calculate the distance to your thumb in centimeters. Make sure to use the proper formula!

4. Measure the true distance using a meter stick. Compare the two values using the percent error formula.