Resources: Wolfram Alpha

Demonstrations: Scale of the Universe, TA Brandon Bergerud's Interactive Planets Demo

In this exercise, you and your lab group will create a scale model of the Solar System, either in the classroom (in-person labs) or on a piece of paper (online labs). Wolfram Alpha may prove useful for looking up information and later doing calculations. For example, try typing in "Venus radius in Earth radii".

The scale for the planet separations in the in-person lab is 1:1 billion. The image above shows ten balls of different sizes from the in-person lab, also scaled relative to one another. though on a different scale than the separations and distances at 1:1 billion. These balls represent the eight planets, the dwarf planet Pluto, and the Moon. The Sun is not shown in this picture or represented in this model.

The scale for the planet separations in the online lab is 1:20 trillion. One trillion is one thousand billions (1,000,000,000,000, or 1x10¹²). On this scale, the Sun is less than a tenth of a millimeter in diameter, smaller than the period at the end of this sentence. In this model, you couldn’t see any of the planets without a very strong magnifying glass!

Ratio of Volumes Example

The following word problem uses the same math methods as one of the problems in today's lab. Once you are familiar with the math method, apply it to the problem in your lab. 

The hottest, largest stars in our Solar System have radii five times the radii of our Sun, an average-temperature star. How many Suns would fit inside one of these hot large stars?

In this problem, we are asked a ratio of volumes question. We can assume spherical geometry of these stars, and we are asked to determine how many times larger one of these hot stars is than our Sun, or how many Suns can fit into one of these hot large stars. For this problem, we need to know the equation of the volume of a sphere, which is 4πr³/3. Begin the problem by writing a ratio of two volumes, with the bigger volume on top so it is 'divided up' to see how many of the smaller volumes will fit into it: 

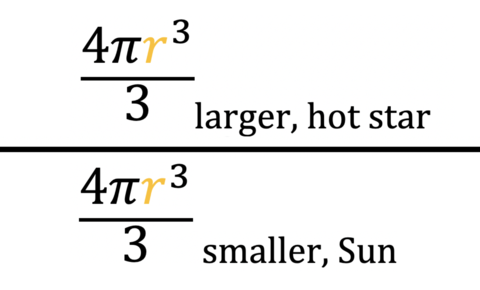
The larger, hot star is our numerator and the smaller Sun is our denominator. We now want to substitute in the value of the larger, hot star's radius (five times the radius of the Sun, or 5R_Sun) for the radius r (in gold) in the equation numerator, and substitute in the value of the smaller Sun's radius (R_Sun) for the radius r in the equation denominator (also in gold). Next, we can cancel out some values the numerator and the denominator have in common.

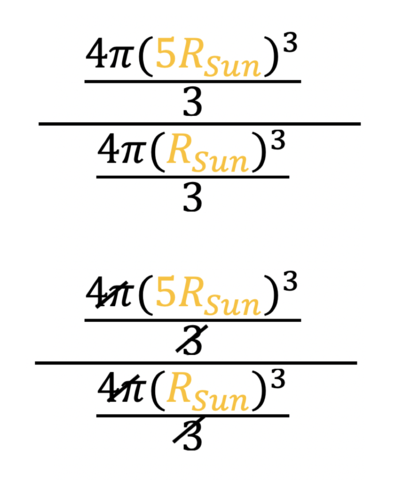
Now we can remove what we canceled and rewrite our equation. Using a property of fractions, we can next simply the equation further. Finally, we can cancel out more values the numerator and denominator have in common. 

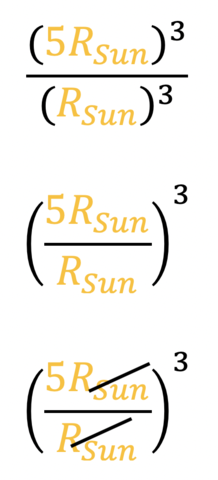
We are left with 5³ = 125 Suns could fit in one of these large, hot stars.